「ハンドルを切ると、なぜ、車は曲がるのか？」…そのプロセスの実態解明。

運転を楽しむ快感は、単純にスピードとか加速という面にもあるのですが、そのハイライトは、やはりコーナリング時の人馬一体感だと思います。読者の皆さんも、だからこそ、足回りやボディ剛性などのチューニングに興味を持たれる方が多いのでしょう。しかし、車がコーナーを曲がるプロセスでは、自動車工学という意味でも、動的感性という視点でも、複雑な要素が絡み合っており、そんなに簡単に性能アップの特効薬を見つけることはできません。あえて言えば、いちばん重要なのは、その車の基本レイアウト(特に重心位置の設定)ですが、それは設計者だけの特権です。量産車をチューニングするという意味では、まず、基本設計のいい車を見極めていただくのが最良の選択だと思います。その上で、ご自分の感性に合わせて味付けをする、もしくは完成度を高めて行くのが、正しいチューニングの方法と言えましょう。
そのための基礎知識として、今回は、コーナリングの基本となる「曲がる」という性能にスポットを当てて解説することにします。


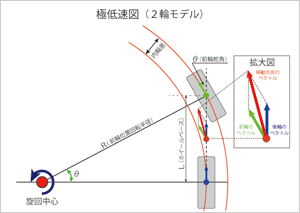
低速での車の曲がり方

皆さんは、普段より何気なく愛車を運転し、操舵して、車を曲げるという動作を行っていますが、「なぜ、車が曲がるのか？」ときかれれば、「ハンドルを切ると、タイヤの向きが変わって、その方向に車が進むから。」とおっしゃる方も多いと思います。その通りです。しかし、それはごく低速、例えば車庫入れの時などのことで、一般的に言えば、ステアリングを切っただけでは、車は意図通りには曲がりません。旋回に伴う遠心力が発生するからです。で、そのことは順を追ってお話しするとして、先ずは、あくまでも例外的な状況ですが、遠心力が働かない場合の曲がり方から見ていくことにします。(説明が複雑になるので、以後、基本的に「２輪モデル」で図示します。トレッドが極端に狭い車という想定です。)

頭の中にイメージしてみてください。ここに一台の車が、左右どちらでもよいのですが、ステアリングを据え切りした状態で置かれています。少しアクセルを踏み込みトラクションを発生させます。すると車は少しずつ動き始め、フロントタイヤの転がる方向へ曲がって行きます。４輪の転がり抵抗に打ち勝つ力のベクトルがあれば、自然にその方向に動いて行くのです。舵角を維持していれば、車はそのまま旋回を始め、図のように前輪の力のベクトル方向と後輪の力のベクトル方向の合算が、矢印赤の方向の力のベクトルとなって、車が移動します。

このように、ごく低速では、遠心力は限りなくゼロに近く、それと釣り合う４輪の向心力(コーナリングフォース)を生み出す必要もありません。だから、結果的には、ステアリングを切った角度に応じて自転しながら公転するというわけです。「運動」の問題というより、むしろ「幾何」の問題として捉えた方が分かりやすいと思います。
念のため付け加えれば、車体の旋回中心は、前輪の舵角とホイールベースによって決まります。
作図から分かるように、Ｌ(ホイールベース) = Ｒ(前輪位置回転半径) X ｓｉｎθ(前輪舵角) ですから、
R(前輪位置回転半径)=Ｌ(ホイールベース)/ｓｉｎθ(前輪舵角)ということになります。

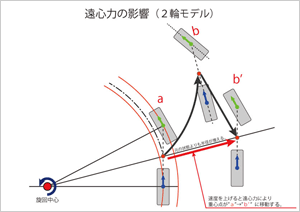
遠心力が働く速度での曲がり方

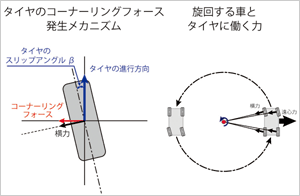
次に、遠心力の影響を受ける速度(３０km/hぐらい以上)での曲がり方について考えてみましょう。この状態では車の速度が高くなっていますから、舵角を与えられた前輪タイヤは、回転方向に転がるだけでなく、車の進行方向に押し出されることになって、接地面が路面との摩擦でギューっと捻じられ、接地面にたわみが生じます。これが連続して捻じられては離れるを繰り返します。その結果、タイヤの進行方向は、タイヤの回転方向に対して、外側にずれて行きます。このずれた角度がスリップアングル（β）です。

ここでタイヤの接地部分で捻じられたコードやゴムが弾性変形をして生み出す力は、タイヤの進行方向に対し直角方向をコーナリングフォースと呼び、タイヤの回転方向に対し直角方向を横力と呼んでいます。コーナリングフォースと横力の間はスリップアングルだけ力の方向が異っているのです。(このように正確にはコーナリングフォースと横力とは区別が必要ですが、スリップアングルは通常では数°以内ですので、力の大きさとしてはほぼ同等です。)この力は車体への向心力として働き、その速度での遠心力を打ち消すことができるという理屈です。 参考として、スリップアングルの発生を実際に検証できる方法をご紹介しておきます。

まず、１０km/h以下の低速で旋回します。一定の旋回半径を維持している状態です。そして、徐々に車速３０km/hを超えるまでゆっくりと加速します。この時、１０km/h以下の低速と同じ舵角では、車はら線を描いて外に向かって膨らんで行きます。車の進行方向が、スリップアングル分外側にずれているからです。（後ほど説明しますが、これはアンダーステアの車の場合です。）右図は、ａ点から車速を上げたことにより、ｂ点に移動したという想定ですが、ｂ点をａ点の旋回角度まで戻してみると、旋回半径が大きくなっていることを示しています。ですから、遠心力が働き出すような旋回運動では、元の旋回半径を維持しようとすれば、矢印赤の分だけのコーナリングフォースを得るために、ステアリングを切り足してやる必要があるのです。 つまり、同じ舵角では低速時の半径では曲がれず膨らんでしまうことで、スリップアングルを認識できるわけです。


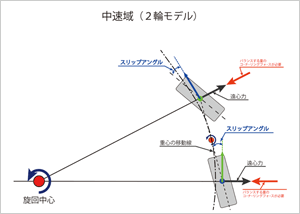
定常円旋回という曲がり方

次に、遠心力が働くコーナリングの状態を、もう少し詳しく見てみることにします。前輪にスリップアングルが生まれ、車体が向きを変え始めると、リアタイヤにも（後輪は車体と一体なので）スリップアングルが発生し、両方にコーナリングフォースが発生することになります。この前後輪のコーナリングフォースと、各輪に働く遠心力がそれぞれバランスする状態になると、車体が一定の半径で弧を描いて曲がるという現象につながって行くのです。車が曲がるためには、前輪と後輪の双方にスリップアングルがつき、タイヤにコーナリングフォースが発生するのが、重要なポイントです。旋回運動と言うと舵輪のみの要因と思われがちですが、前輪と後輪を合計した４輪のコーナリングフォースの総和が、遠心力とバランスしながら、旋回運動を行うのです。

このことを別の視点から説明すると、前輪に発生したコーナリングフォースは、車の重心点に対して内側に回転するヨーモーメント(Z軸まわりに自転させる力)として作用します。ですから、重心点を挟んだ後輪側は、外側に回転することになり、後輪にもスリップアングルがつき、コーナリングフォースが発生するのです。ただし、前後輪のコーナリングフォースは逆向きのモーメントですから、それが釣り合った時点でヨーモーメントは消滅し、その時のヨーレート(自転速度)を保ちつつ、一定の半径を持つ円周にそって公転することになります。このような状態を定常円旋回と言います。ヨーモーメントが働いた時に、スッと回頭するか否かは、以前§9でお話ししたヨー慣性モーメントの大小で決まります。
I＝M　ですから、=M/I という関係です。( I：ヨー慣性モーメント　M:ヨーモーメント　:ヨー角加速度　)
この定常円旋回は、日常の運転で体験することはないと思いますが、現実のコーナーを分解してみれば、様々な半径の円周の一部をつないだものと見ることもできます。実際のコーナリングでは、これに加減速、左右の切り返しといった運動が加わっているわけで、その変化に車がどのように対応するかが、動的感性にとってのポイントと言えるかも知れません。

加速円旋回での曲がり方

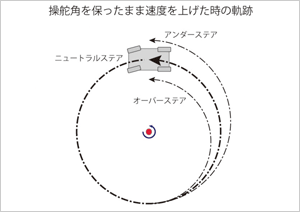
さて、次は、加速円旋回です。定常円旋廻の状態から、舵角を保ったまま速度を上げた時に、車はどのように曲がるか、いわゆるステアリング特性がテーマです。結論から先に言えば、車速の増大につれて旋回半径が大きくなる「アンダーステア」と、逆に旋回半径が小さくなる「オーバーステア」、そして車速が変化しても旋回半径が変わらない「ニュートラルステア」という３種類の特性が、それぞれの車の基本的な性格として存在します。

では、なぜ、そのような違いが生じるのか。以下はかなり専門的な理屈ですが、大体のイメージをつかんでいただけるように、できるだけシンプルにご説明します。
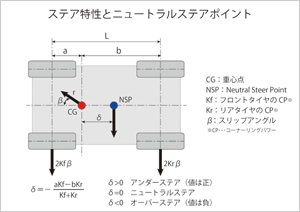
ここで重要になるのが、各輪のコーナリングパワー（ＣＰ）がバランスするポイントです。「ニュートラルステアポイント（ＮＳＰ）」と呼びます。一般の乗用車では、４輪に同じサイズのタイヤを選択されているケースが多く、ＮＳＰは、Ｘ軸上のホイールベースの中心点近辺に存在します。そして、このＮＳＰと重心（ＣＧ）までの位置関係でステアリング特性が決まるのです。
( コーナリングパワー： スリップアングル1°当りのコーナリングフォース 単位は[N/Deg] )
図は、前輪が重い（典型的な前輪駆動）車両を表しています。ＣＧの位置が、ＮＳＰより前方にあります。

遠心力は重心に発生しますので、加速をした場合、ＮＳＰと重心までの距離δと遠心力とが曲がろうとする向きとは反対向きのモーメントとして作用し、前輪のコーナリングフォースがバランスできなくなり、旋回半径が膨らむアンダーステアとなります。要するに舵角が不足（アンダー）の状態で、旋回半径を維持するためには、ステアリングを切り足して、もっとスリップアングルを与えて、コーナリングフォースを増やしてやる必要があります。
一方、ＣＧがＮＳＰより後方にあればオーバーステアとなります。同様に加速した場合、重心に遠心力が働きますので、後輪のコーナリングフォースとバランスしきれなくなり、後輪が外に振られることとなります。結果、前輪のコーナリングフォースが後輪より勝っているので、つまり舵角が付き過ぎている（オーバー）ので、少し舵角を戻して（極端な場合は、カウンターをあてて）、コーナリングフォースを減らして、後輪とのバランスを図る必要がある状態です。また、ニュートラルステアは、重心とＮＳＰが一致している状態で、加速旋回においても同一旋回半径を維持することができます。ここで重要なことは、アンダーステアやオーバーステアの特性の車を加速しながら旋回させるためには、NSPをＣＧに一致させるということです。そうするために、操舵角を増やすか減らすかの違いです。ニュートラルステアは、最初の舵角のままでＣＧとＮＳＰが一致しているのです。

参考までに、これらの関係をもう少し工学的に、式で表すと上図のようになります。δ＝０の場合は、式の分子が０となる時で、典型的な例としては、ａ、ｂとＫｆ、Ｋｒがそれぞれ同じ値であれば、δ＝０となります。つまり、重心が５０：５０の車両中心にあり、前後のタイヤのコーナリングパワーが同じ場合で、ＣＧとＮＳＰが同じ点に存在しています。δ≻０の場合は、図のように、重心ＣＧがＮＳＰ前方にある場合で、ａの値が小さくなりますので、分子の[ａＫｆ－ｂＫｒ]の値は負の値となり、δは正の値となり（式が負の値だから）、アンダーステアとなります。 オーバーステアの場合は、逆に、[ａＫｆ－ｂＫｒ]の値は正となり、δは、負の値となります。

気持ちの良い曲がり方とは？

今回は車の操縦性にとっての基礎とも言うべきテーマですから、どうしても自動車工学的な解説が多くなってしまいました。本来の動的感性工学を論じるには、旋回による荷重移動とか、ロール剛性とか、タイヤの特性など、まだまだ重要なファクターが残っているのですが、それらは次回以降でお話しするとして、とりあえずヨー関係での動的感性に影響する因子をまとめてみます。人馬一体感、自らの体の延長とも感じられる車との一体感…そういう気持ち良さを「車の曲がり方」に求めるとしたら、何が問題かということです。
そのひとつは、ステアリング特性です。工学的にはニュートラルステアがベストと思われそうですが、感性的には違います。一般的にも言われることですが、むしろ適度な弱アンダーな特性を、ステアリングで補正しながら曲がる方が安全かつ気持ちがいいと思います。量産車のチューニングでは、基本的な特性を変えることはできませんが、タイヤの選択などで多少の変化を求めることは可能でしょう。

次は、ステアリング操作に対する回頭性の速さです。基本的にはヨーモーメントによる角加速度の大きさが影響し、それは、本文中にも記したように、その車固有の慣性モーメントに支配されますが、ステアリング系の剛性やギア比による感覚的な影響もありますから、その意味では多少のチューニングは可能でしょう。角加速度が速ければ、ステアリングを回した時にスパッと素早く向きが変わり、感性としてはシャープなハンドリングと感じることになります。
ハンドリング感覚に影響するものとしては、もうひとつ、ヨー角固有振動数というものがあります。これもその車固有の工学的性能ですが、感覚的に理解するとしたら、以下のようなイメージです。実際に試すのは危険ですから、あくまでもバーチャルな世界で想像してみてください。
広い安全な広場で、一定速度で直進している時、ステアリングを９０°程度操舵して手を離してみてください。車速は保ったままです。すると、車は左右に振られて振動状態になります。やがて、振動が減衰し、収束して、再び直進走行に戻ります。この左右に振られる現象がヨー角固有振動です。周波数は0.7～1.2Hz程度とされています。振動数が速いということは、短時間でストロークし、ヨー角速度が速くて、ヨー角加速度も高い値となり、車においては回頭性が機敏で、シャープなハンドリング特性を得ることができるということです。平たく言えば、ハンドルを切った時の向きの変わり易さ、戻り易さということです。
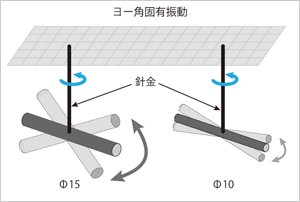
固有振動数については、多分、皆さんがこれ以上詳細に理解される必要はないと思いますが、参考のために、疑似的な実験モデルを紹介しておきます。

針金の上部を固定して、その先端にΦ１５の鉄筋を水平に吊り下げたものを想像してください。これを例えば、右回りに少し捻じって（舵を加える）、手を離してみてください。鉄筋は左へ回り、次にはある点で止まり、右に回りだします。これを数回繰り返すことになります。１秒間に何回振れるか、これがヨー角固有振動数です。次に同様に同じ長さの細くて軽い、Φ１０の鉄筋を吊り下げて、同じように捻じって離します。今度は、振れる周波数が速くなります。両者では、重量が異なるので軽い方が、ヨー慣性モーメントが小さいため、振動数も速くなるのです。この実験での、針金・鉄筋・捩じる力は、車に戻せば、針金はタイヤのＣＰ、鉄筋は慣性モーメント、ねじり力はスリップ角に相当します。

以上、今回も理屈が多くなりましたが、それぞれのキイワードをネットで検索すると多くの解説がヒットします。分かりにくいところがあれば、信頼できそうなサイトを選んで、参照してみてください。
ロール剛性など、コーナリングに関するその他の工学的な問題は、次回以降にお話しする予定です。 引き続きご愛読の上、お役立てください。